Abstract
FROG: Frobenius-guided Relevance Optimization with Guided noise for Efficient Fine-tuning of Large Language and Vision Models
This paper introduces FROG (Frobenius-guided Relevance Optimization with Guided noise), an innovative approach for efficient fine-tuning of large language models (LLMs) and vision models (VLMs). FROG combines SVD-based weight relevance scoring, Frobenius norm-based matrix importance calculation, and dynamic noise injection to significantly reduce the number of trainable parameters while maintaining model performance. This method enables faster and more resource-efficient fine-tuning of large pre-trained models for specific tasks.
1. Introduction
As LLMs and VLMs continue to grow in size and complexity, fine-tuning these models for specific tasks becomes increasingly challenging due to computational and memory constraints. FROG addresses this challenge by intelligently selecting a subset of weights to fine-tune based on their relevance and the importance of their respective matrices. This approach not only reduces the computational requirements but also helps maintain the pre-trained knowledge while adapting to new tasks.
2. Background
Fine-tuning large pre-trained models has become a standard practice in transfer learning for natural language processing and computer vision tasks. However, traditional fine-tuning methods often require updating all model parameters, which can be computationally expensive and may lead to catastrophic forgetting. Recent research has focused on parameter-efficient fine-tuning methods, such as adapter layers and sparse fine-tuning, to address these issues.
The FROG method builds upon the intuition that not all weights in a neural network contribute equally to the model’s performance. By analyzing the structure of weight matrices through SVD, we can identify the most influential weights and focus the fine-tuning process on these parameters.
3. Methodology
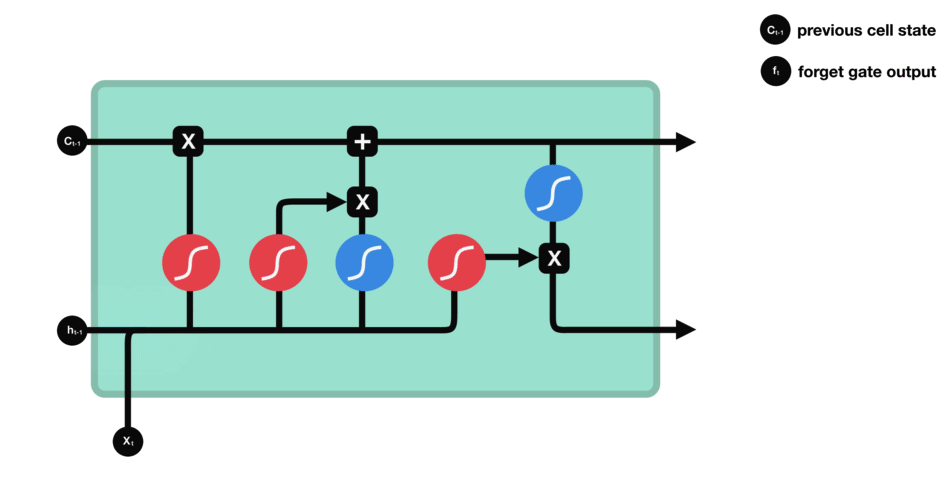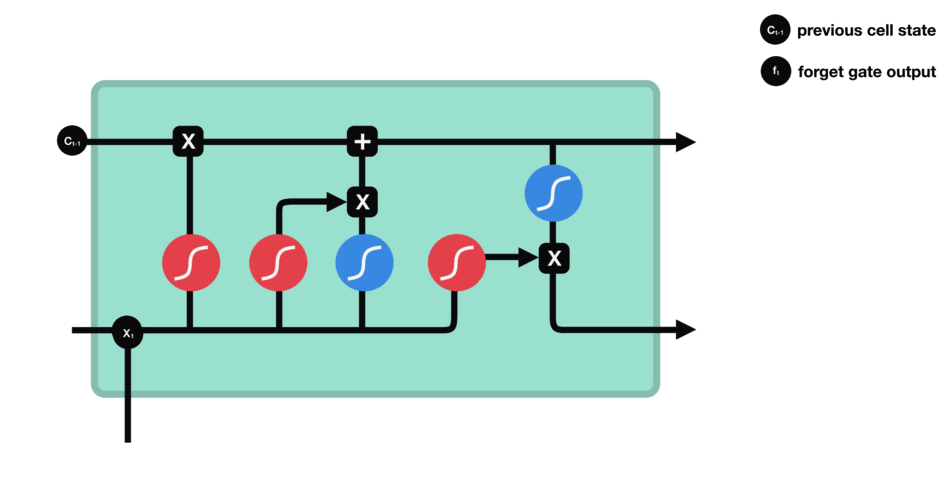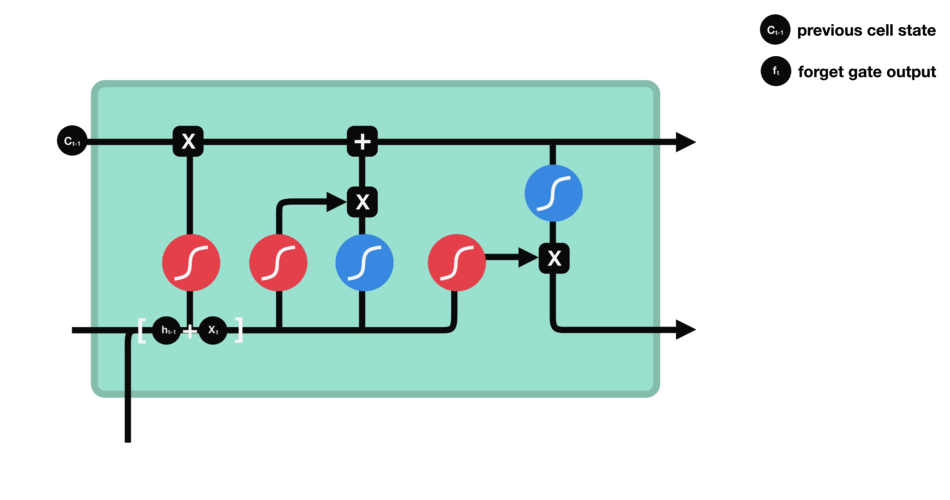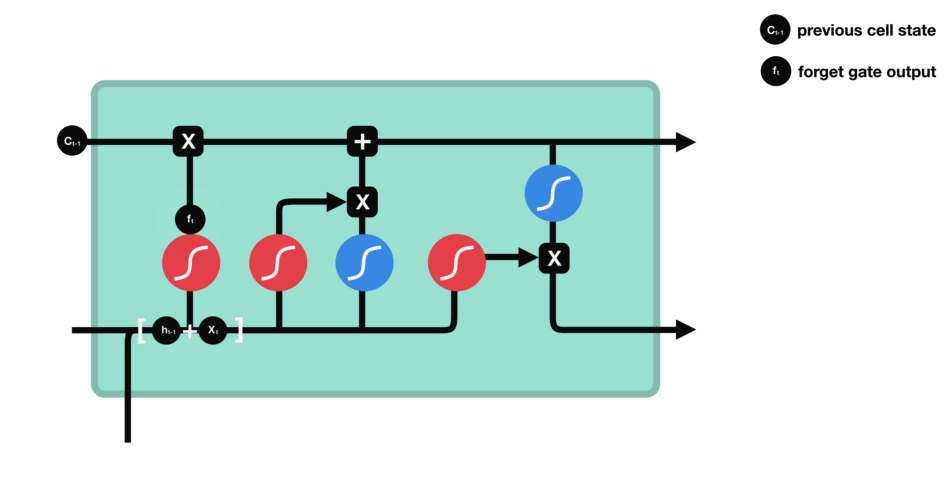
3.1 SVD-Based Weight Relevance Scoring
The weight relevance scoring in FROG is based on the SVD decomposition of weight matrices and the relationship between weights and singular values. This approach considers the weight’s impact on the overall transformation performed by the weight matrix.
For each weight matrix W in the model:
- Perform Singular Value Decomposition (SVD): W = UΣV^T
- Calculate weight relevance scores:
S_ij = Σ_k (σ_k * |u_ik * v_jk|)
where:
- σ_k is the k-th singular value
- u_ik is the (i,k) element of U
- v_jk is the (j,k) element of V^T
- The sum is taken over all ranks k
This scoring method computes the relevance of each weight by summing its contributions across all singular value components. Weights that contribute significantly across multiple components will have higher relevance scores.
The absolute value is used to focus on the magnitude of the contribution, regardless of its direction. This approach ensures that we capture the full importance of each weight across the entire transformation represented by the weight matrix.
3.2 Derivative-Based Weight Initialization
Initialize trainable weights based on their relevance scores:
w_ij_init = α * S_ij * N(0, 1)
where α is a scaling factor and N(0, 1) is a standard normal distribution
This initialization scheme ensures that the initial values of the trainable weights are proportional to their relevance scores, allowing the most important weights to have a larger initial impact on the fine-tuning process.
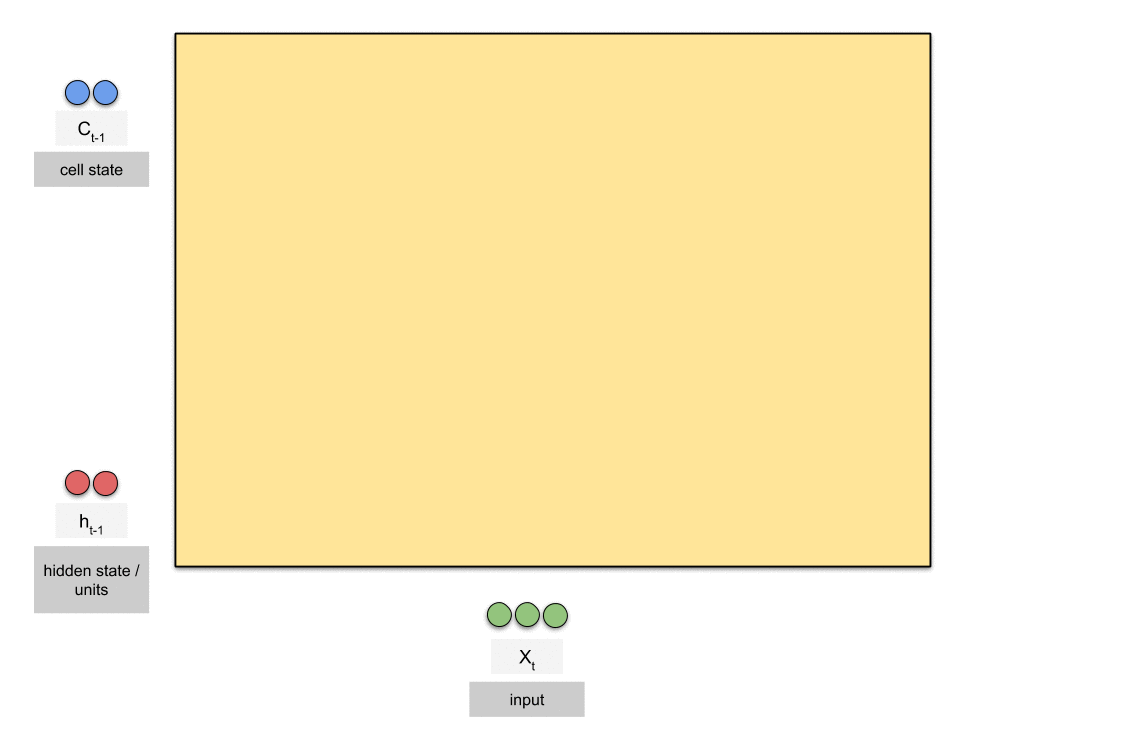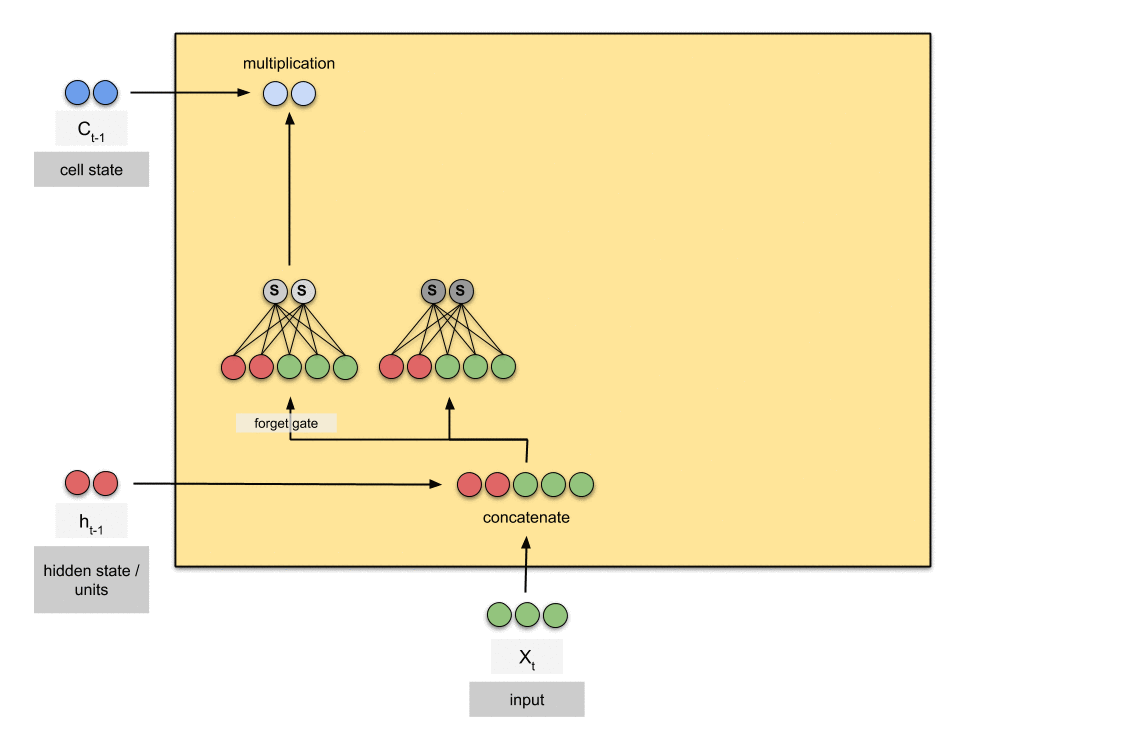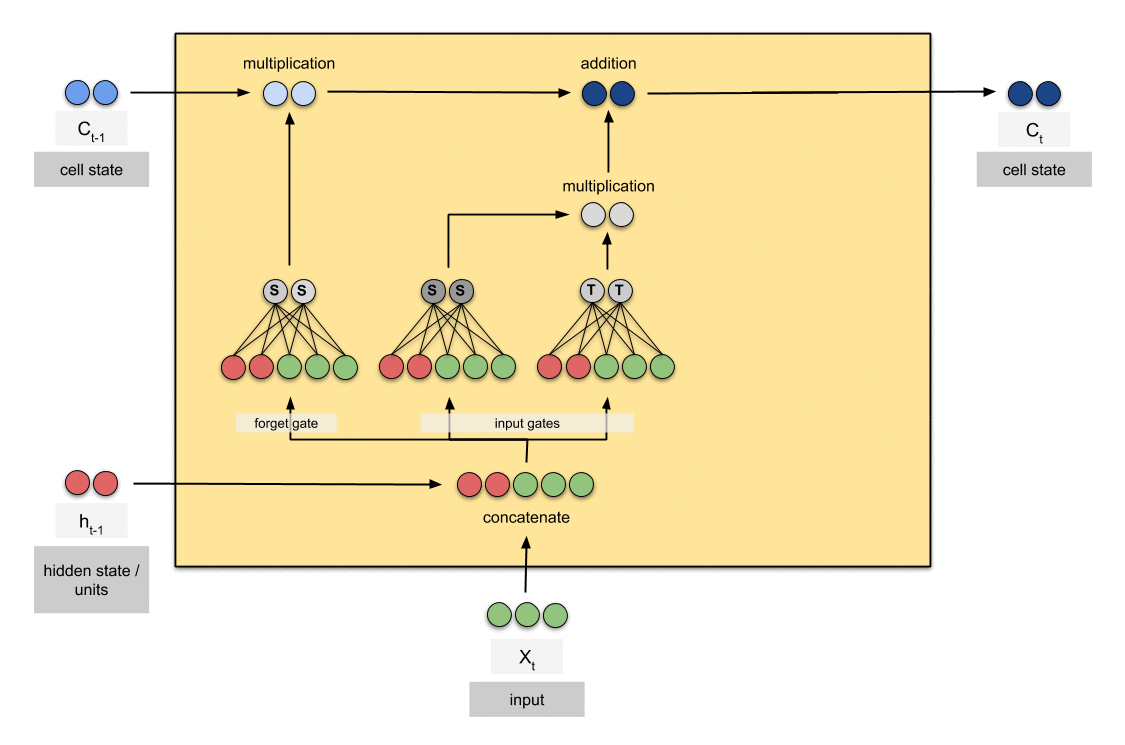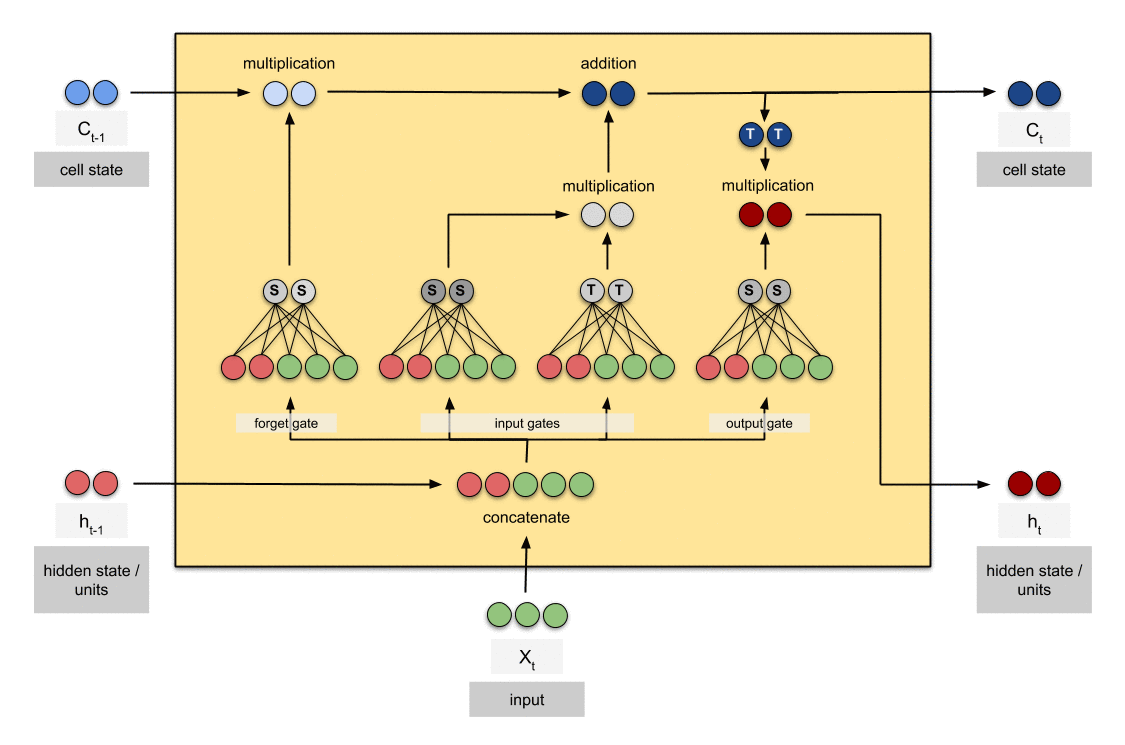
3.3 Training Process with Dynamic Noise Injection
During training:
- Update trainable weights using standard optimization techniques
- Apply dynamic noise injection to frozen weights:
W_frozen = β * S_ij * N(0, σ_noise)
where β is a scaling factor and σ_noise is the noise scale
The dynamic noise injection serves two purposes:
- It helps maintain the plasticity of the frozen weights, allowing them to contribute to the model’s adaptation despite not being directly updated.
- It acts as a form of regularization, potentially improving the model’s generalization capabilities.
3.4 Matrix Importance Calculation using Frobenius Norm
After applying the FROG method to individual matrices:
- Calculate the Frobenius norm for each weight matrix W_i:
||W_i||_F = sqrt(sum(σ_j^2))
where σ_j are the singular values of W_i obtained through SVD - Compute the relative importance R(W_i) of each matrix:
R(W_i) = ||W_i||_F / sum(||W_j||_F for all j)
3.5 Distribution of Trainable Weights
Given a global percentage G% of trainable weights:
- Calculate total number of weights: T = sum(size(W_i) for all i)
- Determine total trainable weights: T_trainable = G% * T
- For each matrix W_i:
- Trainable weights for W_i = round(T_trainable * R(W_i))
- Percentage of trainable weights for W_i = (Trainable weights for W_i / size(W_i)) * 100%
4. Implementation
4.1 Preprocessing
- Perform SVD on all weight matrices of the pre-trained model
- Calculate Frobenius norms and relative importance for all matrices
- Distribute the global percentage of trainable weights across matrices based on their relative importance
- For each matrix W_i:
- Apply the FROG method as described in sections 3.1-3.3
- Select top P_i% of weights to keep trainable, where P_i is the percentage determined for matrix W_i based on its relative importance
- Implement efficient SVD computation, potentially using randomized SVD algorithms for very large matrices to reduce computational overhead
4.2 Fine-tuning
- Initialize trainable weights using the derivative-based method
- During training:
- Update trainable weights using standard optimization techniques
- Apply dynamic noise injection to frozen weights
- Monitor performance on validation set and adjust hyperparameters as needed
- Implement gradient checkpointing or other memory-efficient techniques to handle large models if necessary
- Use mixed-precision training to further reduce memory requirements and speed up computations
5. Advantages
- Significant reduction in trainable parameters, enabling faster and more efficient fine-tuning
- Preservation of pre-trained knowledge through selective weight updating
- Adaptive distribution of trainable weights across matrices based on their relative importance
- Dynamic noise injection to maintain model plasticity and prevent overfitting
- Scalability to very large language and vision models
- Intuitive approach based on the approximation of weight importance through SVD analysis
- Potential for improved generalization due to the combination of selective weight updating and dynamic noise injection
6. Considerations
- The global percentage G% of weights to keep trainable can be adjusted based on the specific fine-tuning task and model size
- The distribution of trainable weights across matrices may need to be monitored to ensure balanced fine-tuning across the model
- Hyperparameters such as noise scale and learning rate may require task-specific tuning
- The effectiveness of the SVD-based relevance scoring may vary depending on the architecture and depth of the model
- For very large models, the initial SVD computation may be computationally expensive, requiring efficient implementation or approximation techniques
7. Future Work
- Investigation of the impact of Frobenius norm-based matrix importance on fine-tuning performance across different model architectures
- Exploration of alternative matrix importance metrics and their effects on weight distribution
- Integration of FROG with other parameter-efficient fine-tuning techniques, such as adapter layers
- Application of FROG to multimodal models and cross-modal transfer learning tasks
- Investigation of the relationship between weight relevance scores and actual gradients during fine-tuning to further validate and potentially improve the scoring method
- Exploration of adaptive noise injection techniques that adjust based on the training dynamics and relevance scores
8. Conclusion
FROG presents a novel approach to efficient fine-tuning of large language and vision models by combining SVD-based weight relevance scoring, Frobenius norm-based matrix importance calculation, and dynamic noise injection. This method significantly reduces the number of trainable parameters while maintaining model performance, enabling faster and more resource-efficient adaptation of large pre-trained models to specific tasks. The incorporation of Frobenius norm-based matrix importance allows for a more nuanced distribution of trainable weights across the model, potentially improving the efficiency of weight selection for fine-tuning. As the field of AI continues to advance with increasingly large and complex models, techniques like FROG will play a crucial role in making these models more accessible and adaptable to a wide range of applications.
9.Visualizing Layer Importance in FROG
While our initial analysis focused on the global percentage of selected weights across the entire model, it’s crucial to understand the importance of individual layers. The FROG method inherently calculates a matrix score for each layer, which provides a direct measure of layer importance.
Layer Importance Visualization
To gain deeper insights into the model’s structure and the relative importance of each layer, we propose a simple yet effective visualization:
Bar Graph of Layer Importance:
- X-axis: Layer numbers (1, 2, 3, …, n)
- Y-axis: Matrix score (importance score) for each layer
- Each bar represents a layer, with its height indicating the layer’s importance score
This visualization offers several benefits:
- Clear representation of relative layer importance
- Easy identification of the most and least critical layers
- Insights into the model’s architectural significance
Interpretation and Implications
By examining this layer importance graph, we can:
- Identify critical layers that contribute most significantly to the model’s performance
- Detect patterns in layer importance across the model’s depth
- Inform more targeted fine-tuning strategies, such as:
- Applying different learning rates to layers based on their importance
- Selectively freezing or unfreezing layers during fine-tuning
- Guiding pruning decisions for model compression
Future Directions
This layer-specific analysis opens up several avenues for future research:
- Investigating the relationship between layer importance and model performance on specific tasks
- Developing adaptive fine-tuning algorithms that dynamically adjust based on layer importance
- Exploring how layer importance changes during the fine-tuning process
By incorporating this layer importance analysis, we enhance our understanding of the model’s internal structure and can potentially develop more efficient and effective fine-tuning approaches.
10. A Global Approach to Weight Selection and Layer Importance
While our current method selects weights independently within each layer, we propose an alternative approach that could offer new insights into the global importance of weights across the entire model.
Global Weight Selection
Instead of selecting a percentage of weights from each layer individually, we suggest ranking all weights across the model and selecting the top X% globally. This approach has several potential implications:
- Uneven Distribution: Some layers may contribute more weights to the selected set than others, potentially revealing which layers are globally more important.
- Dynamic Layer Importance: As we increase the global percentage of selected weights, the relative importance of layers could shift, providing insights into the model’s hierarchical structure.
- Cross-Layer Connections: This method might uncover important weight connections that span multiple layers, which could be missed when analyzing layers in isolation.
Redefining Layer Importance
In this global selection framework, we can redefine layer importance as follows:
- The importance of a layer would be calculated as the sum of scores of its weights that are selected in the global pool.
- Layers with more weights in the globally selected set would be considered more important.
This redefinition could lead to a more nuanced understanding of how different parts of the model contribute to its overall function.
Potential Insights
This global approach to weight selection could offer several advantages:
- Holistic Model Understanding: By considering all weights together, we might gain a more comprehensive view of the model’s internal dynamics.
- Architecture-Sensitive Analysis: This method could be more sensitive to the overall architecture of the model, potentially revealing design insights.
- Adaptive Fine-Tuning Strategies: Understanding which layers contribute more to the globally important weight set could inform more targeted fine-tuning approaches.
Considerations for Future Exploration
By exploring this global weight selection approach, we may uncover new perspectives on model structure and function, potentially leading to more efficient and effective fine-tuning strategies.
Author : Loic Baconnier